数列の極限の基礎は何か．

数列の極限において，基礎は何か．

　数列の極限の学習において，最低限計算できなければならない（基礎）は以下の２つである．

1. 第項が計算できる．
   • 第項の計算とは，自然数に対応する数()をで表すこと．
2. を求めることができる．

　これらができれば後は応用なので，自分で考えたり，問題のパターンを整理することになる．

なぜこの２つなのか．

　極限は未定義の対応関係を定めることである．したがって，数列の極限は自然数がのとき（未定義）の対応関係を定めるのである． そのために第項をで表し，これをもとにして対応値を推定・定めることになる．

自然数と数列の対応関係

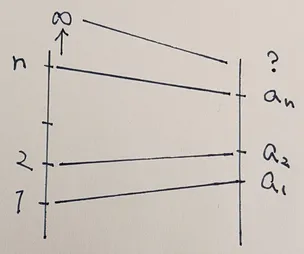
　もう少しだけ詳細に説明する．数列は自然数とそれに対応する数の対応関係と見ることができる．自然数にはないので，第項に現れるを大きくすることで 対応値を推定し，それに定めることになる．したがって，自然数に対応する第項をで表し（計算し）， 自然数をとてつもなく大きく（）したときの対応値を求めることが基礎になる.

第n項の計算の基礎は何か．

　等差・等比関係をもとに第項をで表す（計算する）ことが基礎となる．高校数学では等差数列もしくは等比数列（第項と第項の関係が等差か等比） しかない．つまり，である．この等差・等比関係をもとに第項を計算できればよい．（計算方法は別のいろいろなところで 解説されているので，そちらを参照願う．）

第項の計算の基礎

　学習が進むと，級数についても計算することになる．これも第項と第項の関係が等差・等比しかないので，基礎ができれば問題はない．第項が計算できれば， を求めるだけだから．

n → ∞の計算の基礎は何か．

　上で書いたとおり，極限は未定義の対応関係を定めることなので，数列においてやることはしかない．そしてこの計算の基礎は以下となる．

n → ∞の計算の基礎

　は説明が必要である．これが言いたいことは，のとき，分子と分母を比較すると 分母が分子を無視できるほど大きくなる形に変形して，にすることである． 例えば，

は分母が分子よりとても大きくなるので，に収束する．変形してにするということは，

ということ．