関数の極限と微分の基礎は何か．

なぜ，関数の極限が基礎なのか．

　基礎となる計算は，関数の分母が $0$ になるようなものが計算できるようになることである．数列の極限の基礎は何か.でも書いたが，極限の計算は未定義の値に対応する値の計算である．関数で例えると， $x = 0$ に対する $\frac{1}{x}$ の値（これは $\infty$ だけど）の計算のことになる．学習が進むと微分

\lim_{x \to a} \frac{f(x)-f(a)}{x - a}

を計算することになり，これは分母が $0$ となる．よって，関数の極限は分母が $0$ になる分数の計算が基礎になる．

具体的にはどんな計算が基礎なのか．

　関数の極限の基礎計算は具体的にはどのようなものができればいいのか，以下に示す．

\begin{gather} \lim_{x \to 0} \frac{\sqrt{x+4}-2}{x} \\ \lim_{x \to 2-0} \frac{1}{(x-1)(x-2)} \\ \lim_{x \to 0} \frac{|x|}{x} \end{gather}

(1)は分子を有理化，(2)は部分分数分解，(3)は右極限・左極限の場合分けによって解くことができる．例えばこれらの計算できれば，基礎計算は問題ないだろう．（この３つだけが基礎をすべてカバーしているとは思わないが．）

関数の極限と微分は何がしたいのか．

　ここの目的はさまざまな関数を微分できるようになって，関数（グラフ）の形を明らかにすることである．

　微分は連続性を使って，局所的になめらかなのか角ばったものなのかを明らかにする．それを統合すると，グラフの全体像が見える．微分は分数の形をした関数の極限なので，関数の極限を計算できないと話にならない．

ここの応用は何か．

　関数の極限と微分において，連続性の性質を使ったものが応用となる．関数（グラフ）がつながっているのは，関数が連続であることを示せばいいし，微分可能性は微分の連続性を示せばいい．連続性が問われるものは応用である．

微分は平均変化率ではない¹．

（ここは読まなくてもよい．）

　位相空間の立場からすると，微分はグラフの集合の形を明らかにすることが目的となる．位相空間の具体化の１つは座標空間（座標平面）なので，微分を平均変化率ととらえると説明しづらくなる．

　では何かというと，微分はグラフの近似を表す．具体的には，ある区間のグラフの形を直角三角形の斜辺にあたる直線で近似する．

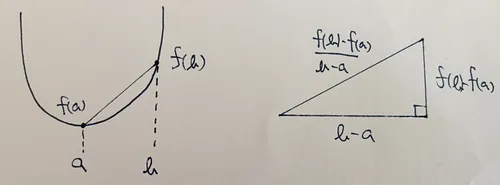
区間を小さくしよりより近似にして，それを集めて全体でみるとグラフの形が明らかになる．

いろいろな参考書は「微分は平均変化率である」という立場．微分を私のようにとらえる人は他にいるのか不明である． ↩