行列は写像と捉える.
行列は複数の数の組の間の対応関係を表す.
多項式は数である.
Section titled “多項式は数である.”多項式は数である.2元1次多項式を例に考える.2元1次多項式とは、2つの変数(例えば)と定数から作られる式で, 各変数の次数が1であるものを指す.つまり,のような形で表される. このは実数や複素数などを表す数の代表である.それら数が和積で表された2元1次多項式は数である. つまり,2元1次多項式に限らず,多項式は数なのである.
多項式は写像1である.
Section titled “多項式は写像1である.”多項式は複数の数の組と1つの数の対応関係を表す写像でもある.2つの変数に対して, という多項式(数)を対応させると,これはのように写像とみることができる.
連立多項式は複数の写像から成る.
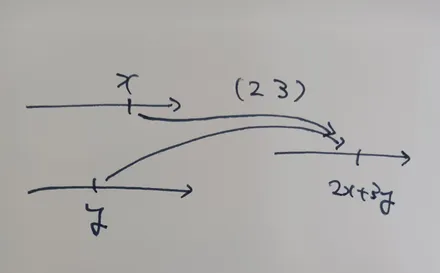
Section titled “連立多項式は複数の写像から成る.”多項式は写像なので,それを連立させた連立多項式は複数の写像ということになる. 例えば,2つの変数に対し,2つの多項式(数)を対応させることを考えると, 1つはに対応する写像,もう1つはに対応する写像となる.
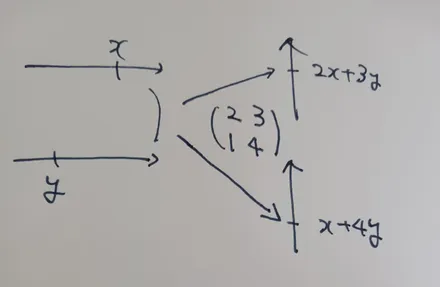
これはとても独自性がありすぎて,受け入れづらいものと考える. そのため現代の線形代数に寄せた独自性を排除した一般的な書き方を画像で記す.
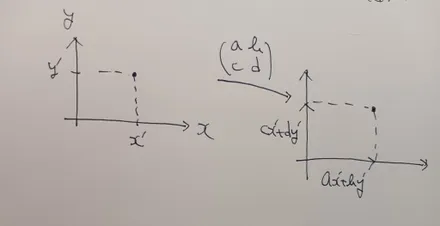
連立多項式と行列表記
Section titled “連立多項式と行列表記”連立多項式を行列を使って表してみる.
行列以外の をベクトルと呼ぶ.縦方向に数が並んでいるものである.
Footnotes
Section titled “Footnotes”-
写像については,他サイトの解説を参考にしてください.知っているものと扱います. ↩