ベクトルの定義
個の数を並べた組を項（または次元）数ベクトルまたは単にベクトルという． それぞれの数をその成分という．
以下のように成分を縦に並べた組，横に並べた組をそれぞれ列ベクトル，行ベクトルという．
ベクトルとベクトル空間の定義．
線形代数を学習していると，行列から始まったけどなぜかベクトルの話に終始する． 連立方程式はどこかへ行き，何をやっているのかまったくわからなくなる． ここでは単にベクトルとベクトル空間について定義する．とてもつまらない記事である．
まずはベクトルを定義．
Section titled “まずはベクトルを定義．”このブログではここまでの線形代数の記事にベクトルを定義せずに使用していた． 線形代数の記事にアクセスする読者はベクトルくらい見たことあると想定しているからだ． しかし，今後の記事ではベクトルも数多く登場すると思うので，一旦定義しておく．
ベクトルの相等
Section titled “ベクトルの相等”２つのベクトル
が等しいとは，それぞれの成分が等しいということ．つまり，
ということ．
ベクトルの演算
Section titled “ベクトルの演算”ベクトルの足し算
Section titled “ベクトルの足し算”ベクトルの足し算は，それぞれの成分を足せばよい．すなわち，2つのベクトルの足し算は
ベクトルのスカラー倍
Section titled “ベクトルのスカラー倍”スカラー倍はベクトルに定数を掛けることだ．つまり，ベクトルのスカラー倍は
ベクトル空間も定義．
Section titled “ベクトル空間も定義．”行列は写像と捉える．で，行列は写像である旨を解説した． 写像であるということは定義域と値域があるはずだが，その辺は濁していた． 定義域と値域はベクトル空間である．ベクトルの集合のことだ．
ベクトル空間の定義
（Geminiに定義を生成させました．）
ベクトル空間 とは、以下の条件を満たす集合と演算（ベクトル和とスカラー倍）の組 () のこと．
1. 和に関する性質
任意のベクトル に対して、
- （和の閉じていること）
- （結合法則）
- （交換法則）
- を満たす零ベクトル が存在する（零ベクトルの存在）
- を満たす逆ベクトル が存在する（逆ベクトルの存在）
2. スカラー倍に関する性質
任意のベクトル とスカラー に対して、
- （スカラー倍の閉じていること）
- （分配法則）
- （分配法則）
- （結合法則）
- （単位元の性質）
ベクトル空間をどう捉えるか．
Section titled “ベクトル空間をどう捉えるか．”ベクトル空間についてどのように考えればいいのかを書く．数学を学習する上でとても大事なことだからだ．
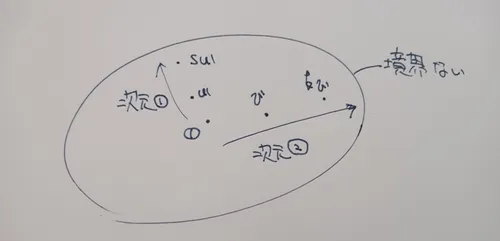
ベクトル空間の捉え方
- ベクトル空間は，零に相等するベクトルを中心として，次元的に広がるベクトルの集まりである．最大・最小のような境界はない．
上のベクトル空間の定義はそれを表している．とても極端に言えば，
- 零ベクトルの存在
- スカラー倍で閉じていること
の２つから「零に相当するベクトルを中心とした次元的に広がるベクトルの集まりがベクトル空間」と言える．
