1次関係
ベクトルが
を満たすとき，これをベクトルの1次関係という． すべてのが0のとき，
はどんなベクトルについても成り立つ． これを自明な1次関係という．
1次関係、1次従属、1次独立についての主張（定義）.
1次関係の主張
Section titled “1次関係の主張”ベクトルの組のとなる関係式のことを１次関係という．関係式さえ満たされれば，係数については気にしない．のとき，どんなベクトルの組でも関係式は必ず満たされるので，関係式は存在するのかを考える必要はない．
ベクトルの組を行列とみれば， が関係式である．（である．） また，を満たすの集合をとすれば，である． （ってなんだよというのは置いておいて．）
1次独立について
Section titled “1次独立について”1次独立
ベクトルの組について，1次関係
が成り立つのは，自明な1次関係すなわち，の場合のみであるとき，は1次独立であるという．
1次独立の主張
Section titled “1次独立の主張”ベクトル空間内の元（ベクトル）を何個か適当に取ってきて，それらを1組と考えた場合，この組の中だけで各元の関係性を調べると，それぞれが独立していると主張している．（独立とは，ある元がその他の元の1次結合で表現できないときをいう．）これを数学的に表現すると，1次関係が自明なもののみ成り立つときが1次独立である．
ベクトルの組のそれぞれのベクトルについて、これらがどのような関係性なのかを主張しているのであって，別のベクトルの組は同じ関係性であるかどうかはわからない（1次従属かもしれない）。
誤って理解してはいけないことは，１組の1次独立のベクトルの数＝次元数，1次独立＝基底ではない．3次元ベクトル空間のある２つのベクトルの組が1次独立であっても，組のベクトル数は次元数とは異なるし，基底になっていない．
１次関係で出てきた集合で言えば，ベクトルの組が1次独立であることはである．これが”1次関係が成り立つのは自明な1次関係の場合のみであるとき”の意味である．
1次従属について
Section titled “1次従属について”1次従属
ベクトルの組が1次独立でないとき，1次従属であるという．すなわちが1次従属であるとは，1次関係 を満たすで，そのうちの少なくとも1つが0でないものが存在するときにいう．
1次従属の主張
Section titled “1次従属の主張”ベクトル空間内の元（ベクトル）を何個か適当に取ってきてそれらを1組と考えた場合，この組が1次独立でないとき1次従属であると主張している．別の言い方をすれば，この組の中だけで各元の関係性を調べると，ある元はその他の元の1次結合で表現できてしまうとき，この組は1次従属であるという．
これも1次独立と同じく，ベクトルの組がどのような関係性なのか（1次独立なのか？1次従属なのか？）を主張している．
1次関係で出てきた集合で言えば，ベクトルの組が1次従属であることはである．すなわち，集合にはゼロベクトル（）以外に元が存在するということ．
もう少し深堀り
Section titled “もう少し深堀り”1次関係はのことで，自明な1次関係を必ず満たし，非自明な1次関係とともに構成される．すなわち，は1次独立と関係するゼロベクトルを必ず含み，1次従属と関係するゼロベクトル以外のベクトルで構成される集合であるとみえる．
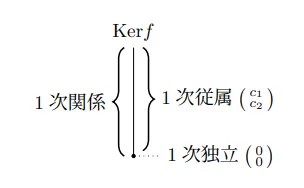
1次関係は関係式のことで，1次独立と1次従属はベクトルの組の各ベクトルの関係性についての主張であり，両者を区別しないと混乱する．
以下の質問に答えよ．
- 1次関係とは何か．
- 1次独立とは何か．
- 1次従属とは何か．
- 1次関係と1次独立・1次従属はどういう関係か．