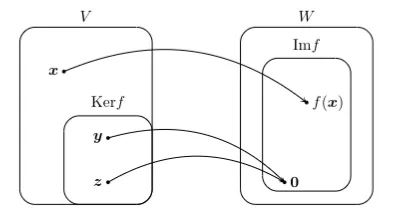
定義6.3.2
をベクトル空間，を線形写像とするとき，をの像空間という．とも書く．また，をの核空間という．
線形写像の像空間と核空間（定義）
通常の写像（の像）と同じことを言っているが，が線形写像のときは像空間と言っている．
が線形写像のとき，に対応する行列が１つ定まる（線形代数を学んでいくと，どこかでその定理を証明することになる．）．すなわち線形写像を１つ定めたとき，それに対応する行列があって，となる．よって， はなるの集合である．
像空間と核空間についての例題（例題13） 像空間と核空間についての例題（例題13）