線形写像と1次結合の行列表記

定理6.3.3

　$V, W$をベクトル空間，$f \colon V \to W$ を線形写像とする．

　$V$の $m$ 個のベクトル $\boldsymbol{u}_{1}, \cdots , \boldsymbol{u}_{m}$，$V$ の$n$ 個のベクトル$\boldsymbol{v}_{1}, \cdots , \boldsymbol{v}_{n}$ と $m \times n$ 行列 $A = (a_{ij})$ が，次の関係を満たしているとする．

$$(\boldsymbol{v}_{1} \cdots \boldsymbol{v}_{n}) = (\boldsymbol{u}_{1} \cdots \boldsymbol{u}_{m}) A$$

すなわち，

$$\boldsymbol{v}_{j} = \sum_{i=1}^{m}a_{ij}\boldsymbol{u}_{i} \quad ( j = 1, \cdots ,n)$$

そのとき，

$$( f(\boldsymbol{v}_{1}) \cdots f(\boldsymbol{v}_{n}) ) = ( f(\boldsymbol{u}_{1}) \cdots f(\boldsymbol{u}_{m}) )A$$

定理の主張

　ベクトル空間 $V,W$ の間に線形写像が定義されている．このとき，$V$の2つのベクトルの組の間に行列 $A$倍の関係があれば、これらに対応する$W$の２つのベクトルの組の間にも行列$A$倍の関係がある．2つのベクトルの組が変われば，行列も変わる．

線形写像と1次結合の行列表>示の関係

定理の仮定と結論

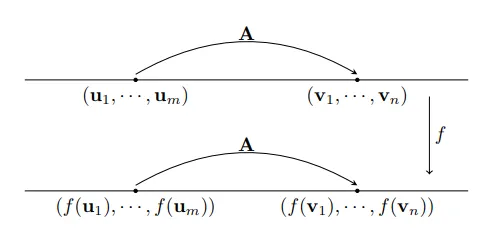
　わかりづらいので，整理する．

仮定A1

$$f \colon V \to W は線形写像である$$

仮定A2

$$(\boldsymbol{v}_{1} \cdots \boldsymbol{v}_{n}) = (\boldsymbol{u}_{1} \cdots \boldsymbol{u}_m)A \space すなわち，\boldsymbol{v}_{j} = \sum_{i=1}^{m}a_{ij}\boldsymbol{u}_{i}$$

結論B

$$( f(\boldsymbol{v}_{1}) \cdots f(\boldsymbol{v}_{m}) ) = ( f(\boldsymbol{u}_{1}) \cdots f(\boldsymbol{u}_{m}) )A$$

証明の考え方

　（結論B）は$\text{２つのベクトル}$が等しいことを主張している．これを示すには、成分同士が等しいことを示せばよい。すなわち、

$$f(\boldsymbol{v}_{j}) = \sum_{i=1}^{m} a_{ij}f(\boldsymbol{u}_{i} ) \quad (j = 1, \cdots , n) \tag{B1}$$

を示す．

（仮定A2）より，$\boldsymbol{v}_{j} = \sum_{i=1}^{m} a_{ij}\boldsymbol{u}_{i}$であることと，（仮定A1）の$f$の線形性から，

$$\begin{aligned} f(\boldsymbol{v}_{j}) &= f(a_{1j}\boldsymbol{u}_{1}+a_{2j}\boldsymbol{u}_{2}+\cdots+a_{mj}\boldsymbol{u}_{m}) \\ &= f( a_{1j}\boldsymbol{u}_{1}) + f( a_{2j}\boldsymbol{u}_{2}) + \cdots + f(a_{mj}\boldsymbol{u}_{m} ) \\ &= f( a_{1j}\boldsymbol{u}_{1}) + f( a_{2j}\boldsymbol{u}_{2}) + \cdots + f(a_{mj}\boldsymbol{u}_{m} ) \\ &= \sum_{i = 1}^{m}a_{ij}f(\boldsymbol{u}_{i}) \quad (j = 1, \cdots , n) \end{aligned}$$

よって，（B1）が示せた．したがって，（結論B）が示せた．