コンテンツにスキップ
数学の主張

線形写像の合成と表現行列の関係について（定理6.10.4）

定理6.10.4

　𝑉,𝑊,𝑈をベクトル空間，𝒗1,⋯𝒗𝑛, 𝒘1,⋯𝒘𝑚, 𝒖1,⋯,𝒖𝑙をそれぞれ𝑉,𝑊,𝑈の基底とする．２つの線形写像

𝑓:𝑉→𝑊,𝑔:𝑊→𝑈

が与えられたとき，上記基底に関して，𝑓,𝑔に対応する表現行列をそれぞれ𝐴,𝐵とすると，合成写像

𝑔⚬𝑓:𝑉→𝑈

に対応する表現行列𝐶は，等式𝐶=𝐵𝐴を満たす．

定理の主張

Section titled “定理の主張”

　合成写像の基底に関する表現行列は，合成している写像の表現行列の積で素直に表せられることを主張している．

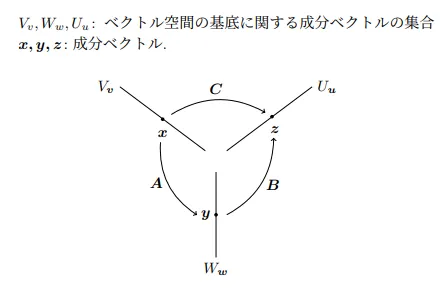
線形写像の合成と表現行列の関係
線形写像の合成と表現行列の関係

証明の考え方

Section titled “証明の考え方”

　𝐶=𝐵𝐴を示すためには，行列Cと行列BAの成分どうしが同じであることを示せばよいが，線形写像の行列表現と成分ベクトルとの関係性から示したほうが簡単そうであるので，そうする．

　ベクトル空間𝑉のベクトル𝒙を基底𝒗1,⋯,𝒗𝑛に関する成分ベクトル(𝑥1⋮𝑥𝑛)，ベクトル空間𝑊のベクトル𝒚を基底𝒘1,⋯,𝒘𝑚に関する成分ベクトル(𝑦1⋮𝑦𝑚)，ベクトル空間𝑈のベクトル𝒛を基底𝒖1,⋯,𝒖𝑙に関する成分ベクトル(𝑧1⋮𝑧𝑙)とする．

　題意から，表現行列と成分ベクトルの関係式は

((((𝑦1⋮𝑦𝑚))))=𝐴((((𝑥1⋮𝑥𝑛)))),((((𝑧1⋮𝑧𝑙))))=𝐵((((𝑦1⋮𝑦𝑚)))),((((𝑧1⋮𝑧𝑙))))=𝐶((((𝑥1⋮𝑥𝑛))))

左の2式から，

((((𝑧1⋮𝑧𝑙))))=𝐵𝐴((((𝑥1⋮𝑥𝑛))))

となる．したがって，一番右の関係式と比較することによって，𝐶=𝐵𝐴となる．