定理7.3.2
線形写像が単射であるための必要十分条件は
定理7.3.2
線形写像が単射であるための必要十分条件は
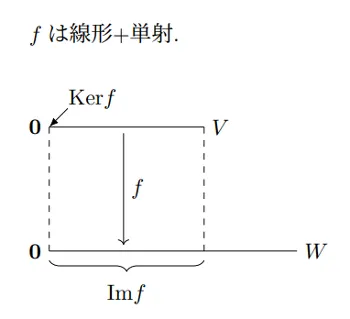
線形写像の単射性を知りたいならば,の元を調べよ.の元(ベクトル)が(ゼロベクトル)のみであれば,は単射である.
線形写像により,に対応するの元が(ゼロベクトル)のみなら,は単射であるということ.
を示す.
は単射であると仮定する.このとき, かつ であることを示せばよい.
を示す.
これは明らか.
を示す.
であることを示す.
とする.このとき,の定義よりが成り立つ.仮定よりは単射なので,を満たすは1つでである.よって,.したがって,.
以上から,.
を示す.
単射の定義より,を示せばよい.
とする.線形性より式を変形して.より,.よって,.したがって,は単射である.