線形写像の単射性と次元の関係について（定理7.3.3（1））

定理7.3.3

　を線形写像とするとき，が単射であるための必要十分条件は

定理の主張

　次元定理からわかるとおり，が線形写像のみの性質を持つならである．しかしこの定理ではが単射なら，との次元が同じになると言っている．（正しくは逆も成り立つという主張．）

線形写像の単射性とベクトル空間の対応関係

線形写像とベクトル空間の対応関係

証明の考え方

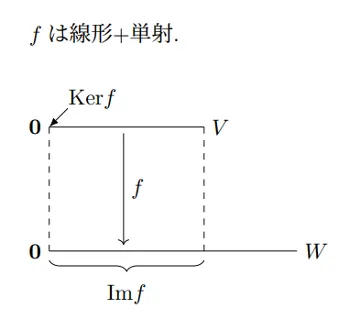
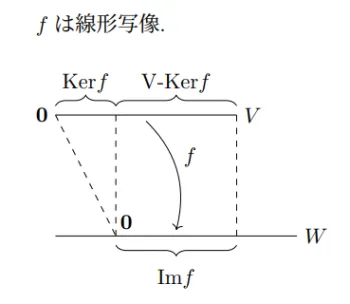
1. が単射

   真正面から証明しようとするなら，かつを示せばよいが，定理7.3.2と次元定理から導出できそう．

   　は単射であるとする．定理7.3.2より．よって，．次元定理より，なので，．

2. が単射

   　こちらも真正面から証明しようとするなら，単射の定義からが単射であること導く．しかし，こちらも次元定理と定理7.3.2から導けそう．

   　とする．次元定理より．これとは線形写像であることより，．定理7.3.2からは単射．

---

復習ノート

• 次元の関係性はが線形のときとが線形＋単射の場合で，どう異なるのか．
• 写像による対応関係，次元との関係を図示できるか．