ジョルダン標準形の主張．

定理12.10.1

　次実正方行列が，重複もこめて個の固有値をもつならば，適当な正則行列によって

はジョルダンの標準形になる．

定理の主張

　固有値の数がベクトル空間の次元と同じなら、ベクトル空間は一般固有空間で分解できる．

一般固有空間の分解

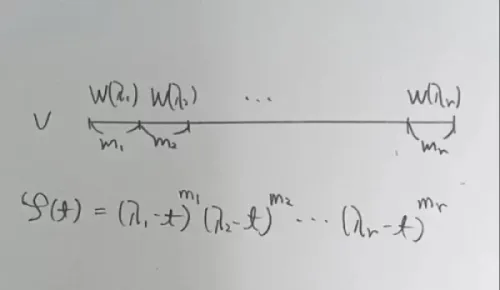
　そして，各一般固有空間はジョルダン・ダイヤグラムを構成する基底で考えると，その表現行列はジョルダン・ブロックで表される．

　適当な正則行列は何かといえば，直和分解した一般固有空間の各ジョルダン・ダイアグラムを順番に並べたものである．

証明の考え方

1. 一般固有空間による直和分解

   　とし，の表現行列をとする．定理12.6.1により，は一般固有空間に直和分解される．つまり，

   すると定理12.1.1より，ある正則行列があって，

   となる．各がジョルダン・ブロックで表されればよい．

2. べき零写像の表現行列を考える．

   　を考える（は恒等写像，f_iの表現行列は）．はでべき零写像である．記述の簡略のため，とおく．

   　このべき零写像のフィルトレーションに関係しての基底をうまく選ぶ．つまり，ジョルダン・ダイヤグラムである．そして，この基底に関しての表現行列を考える．ここにジョルダン・ブロックが現れるからである．

   

   表現行列

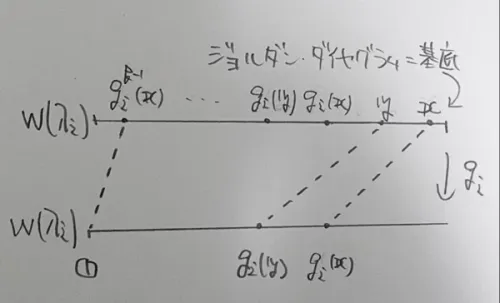
   　表現行列は基底の像と基底との関係であるから，その関係を一部記載すると，

   となる．つまり，表現行列の一部はである．

   表現行列の全体は以下のようになる．

   これをについて解くと，

3. ジョルダン標準形

   　各を(1)に代入すると，はジョルダン標準形となる．

---

復習ノート

　ジョルダン標準形の証明には以下を理解している必要がある．

• 一般固有空間による直和分解．
• べき零写像のジョルダン・ダイヤグラムによる表現行列．