問65
P71 問65 (第3章 数列)
本問は、数列の章の1つ問題として提示されています。つまり、数列の極限の問題です。 したがって、微分や を既知とせず、はさみうちの原理で解きます。
はさみうちの原理には不等式が必要となります。それには を使います。
はさみうちの原理を使って、極限を求めます。そのためには不等式が必要ですが、 単位円を使った面積による不等式を導出します。なので、 下図のとおり第一象限で考えてよいです。
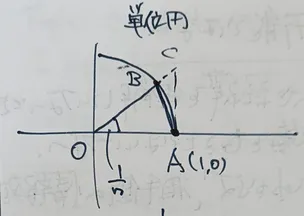
以下の3つの面積を比較します。
- 三角形OAB:
- 扇形OAB:
- 三角形OAC:
図から、面積の大小関係は明らかに 三角形OAB < 扇形OAB < 三角形OAC です。つまり、
これを計算していくと、
となります。
だから、はさみうちの原理より 。