コンテンツにスキップ
数学の主張

有理数の切断と実数(定義1.0，定義1.1)

定義1.0 (有理数の切断)

　有理直線ℚをつぎの2つの条件を満たすように空集合でない2つの部分集合𝐴と𝐴′に分割したとき，𝐴と𝐴′の組を有理数の切断とよび，⟨𝐴,𝐴′⟩で表わす．

  1. 𝑟∈𝐴のとき，𝑠∈𝐴′ならば，𝑟<𝑠.
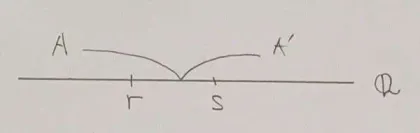
    1.の図的表現
    1.の図的表現
  2. 𝐴に属する最大の有理数はない．すなわち，𝑟∈𝐴ならば，𝑡>𝑟なる有理数𝑡∈𝐴が存在する.
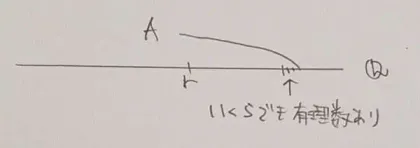
    2.の図的表現
    2.の図的表現

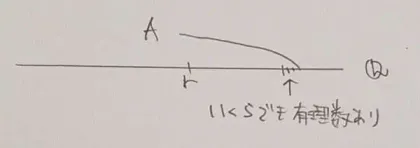
定義1.1（実数）

　有理数の切断を実数とよぶ．

有理数の切断の主張

Section titled “有理数の切断の主張”

　有理数を適当に２つに分けた集合の組が有理数の切断と言っているのではない． 有理数の大小関係を考慮し，一直線上に並べた有理直線を２つに分けたときの， 有理数の無限集合の組を有理数の切断とよぶと主張している．

　ただ，これだと数学的にあいまいなので，この２つに分けた有理数の無限集合の組⟨𝐴,𝐴′⟩は定義の1.,2.を満たすものとする．

　有理数を分割したので，ℚ=𝐴∪𝐴′,𝐴∩𝐴′=∅である．また，切断⟨𝐴,𝐴′⟩において，𝐴の補集合が𝐴′なので，𝐴を決めれば切断⟨𝐴,𝐴′⟩が決まることを意味する．

実数の主張

Section titled “実数の主張”

　有理数とは異なる概念であることを主張している． 有理数の無限集合の組⟨𝐴,𝐴′⟩を実数と考えるため，とても数とはみなせない． しかしこの先，実数の性質をみていくと数とみなしてもよいということになる．

実数の等号

Section titled “実数の等号”

　２つの実数𝛼,𝛽が等しい：𝛼=𝛽というのは，切断⟨𝐴,𝐴′⟩と⟨𝐵,𝐵′⟩が同じであること，すなわち，𝐴=𝐵であることを意味する．

1.と同値な条件

Section titled “1.と同値な条件”

　有理数の切断の条件1.と同値な条件がある．

  • 3. 𝑟∈𝐴に対して，𝑠≤𝑟,𝑠∈ℚならば，𝑠∈𝐴．
  • 3’. 𝑟∈𝐴′に対して，𝑟≤𝑠,𝑠∈ℚならば，𝑠∈𝐴′．

　これら条件は，補集合の関係にある2つの有理数の集合𝐴，𝐴′に分けたのなら，片方が切断の条件を満たせば， もう片方も自動的に条件を満たすから，片方だけ調べればよいということ．

3.の主張

Section titled “3.の主張”

　切断⟨𝐴,𝐴′⟩の𝐴の性質について述べている． すなわち，どんな𝑟∈𝐴に対しても，𝑠<𝑟である有理数𝑠は𝐴に属する．

　逆に考えると，𝐴の性質は𝑠≤𝑟で𝐴に属さない有理数𝑠は存在しないということ． 言い換えると，𝐴の中に𝐴′の元が混ざっていないということ． つまり，以下の図のような切断はない．

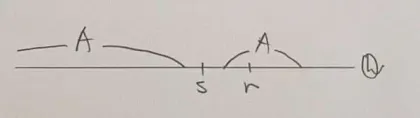
3.の図的表現
3.の図的表現

3’.の主張

Section titled “3’.の主張”

　3.の主張を𝐴′側で考えればよい． すなわち，どんな𝑟∈𝐴′に対しても，𝑟≤𝑠である有理数𝑠は𝐴′に属する．

　こちらも逆に考えると，𝐴′の性質は𝑟≤𝑠で𝐴′に属さない有理数𝑠は存在しないということ． 言い換えれば，𝐴′の中に𝐴の元が混ざっていないということ． つまり，以下の図のような切断はない．

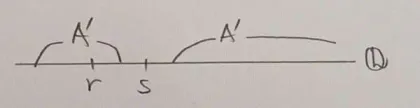
3'.の図的表現
3'.の図的表現

無理数

Section titled “無理数”

　有理数の切断によって，無数の有理数の集合の組𝐴,𝐴′に分けた．定義により𝐴に最大の有理数はない． 𝐴′に最小の有理数が存在しないような組がある．そのとき，この有理数の切断は無理数であると定義する．

　𝐴′に最小の有理数が存在するような組は，有理数である．