コンテンツにスキップ
数学の主張

実数の大小（定義1.2・定理1.1）

定義1.2

　２つの実数𝛼=⟨𝐴,𝐴′⟩,𝛽=⟨𝐵,𝐵′⟩について，𝐴⊊𝐵ならば𝛼は𝛽より小さいといい，𝛼<𝛽と書く．

定理1.1(実数の大小)

　２つの実数𝛼,𝛽の間にはつぎの３つの関係のうちの１つ，そしてただ１つだけが成り立つ．

𝛼<𝛽,𝛼=𝛽,𝛼>𝛽

定理の主張

Section titled “定理の主張”

　有理数と同じく，すべての実数の間には等号含む大小関係が定まる．

証明の考え方

Section titled “証明の考え方”

　𝛼=⟨𝐴,𝐴′⟩,𝛽=⟨𝐵,𝐵′⟩とする．𝐴,𝐵の関係を有理数の切断の性質から考えると，𝐴≠𝐵はありえない．つまり，𝐴⊊𝐵,𝐴=𝐵,𝐵⊊𝐴のいずれかである．

図1
図1

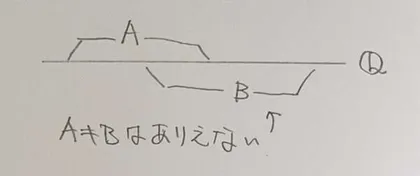
　また，これら３つの関係は集合の性質から，どの２つも両立することはない．つまり，ただ１つだけが成立する．

　𝐴⊊𝐵のとき，定義1.2から𝛼<𝛽．

　𝐴=𝐵のとき，定義1.1の実数の等号から𝛼=𝛽．

　𝐵⊊𝐴のとき，定義1.2から𝛽<𝛼．

復習ノート

Section titled “復習ノート”
  • 実数の定義は何か．