定理1.5
自然数が与えられたとする.このとき,任意の実数に対し,
なる有理数が存在する.
定理1.5
自然数が与えられたとする.このとき,任意の実数に対し,
なる有理数が存在する.
実数は有理数でいくらでも近似できる.近似精度は自然数による.
とする.自然数を何かひとつ決めたとして, なる有理数が構成できることを示せばよい.
有理数を構成する.
を取る.までを分割して,その倍をから加算したものをとおく. すなわち,
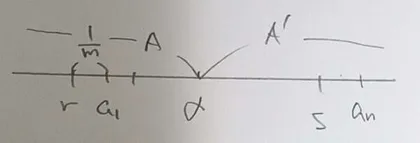
とおく.
は常に有理数で,のときで,のときとなるので, はがから増えるに従い,いつかの元からの元になるはずである.
つまり,から,なる自然数がに存在する.
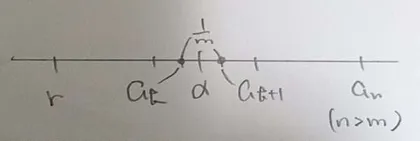
とすれば,なる有理数が存在することになる.